Introduction
Dans le domaine des systèmes automatisés, la régulation des processus est essentielle pour garantir une performance optimale et stable. Parmi les nombreuses techniques de régulation utilisées, la commande RST occupe une place de choix. Elle permet de concevoir des régulateurs offrant à la fois robustesse et précision tout en s’adaptant à une large gamme de systèmes dynamiques. Cet article présente les concepts clés de la commande RST, ses applications, ainsi que ses avantages par rapport à d’autres techniques de commande.
I. Contexte et définitions
A. La régulation dans les systèmes automatisés
La régulation consiste à ajuster les paramètres d’un système afin qu’il réponde de manière optimale aux variations internes et externes. Cette discipline est cruciale dans des domaines aussi variés que l’industrie, l’aérospatiale, l’automobile et les énergies renouvelables.
B. Présentation de la commande RST
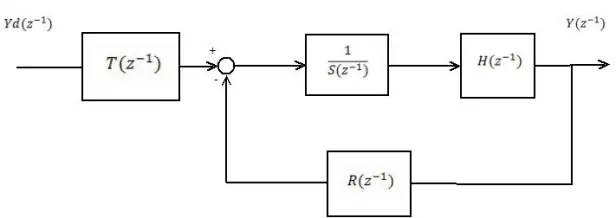
La commande RST est une méthode de régulation qui repose sur trois paramètres : R (régulateur), S (correcteur) et T (commande). Ces paramètres sont déterminés de manière à obtenir une réponse du système conforme à des spécifications prédéfinies. Contrairement à la commande PID (Proportionnelle-Intégrale-Dérivée), la commande RST permet une plus grande flexibilité et s’adapte mieux à des systèmes complexes ou sujets à des perturbations importantes.
II. Les principes de la commande RST
A. Les équations de base
La commande RST repose sur une représentation polynomiale des systèmes dynamiques. Elle vise à modifier le comportement d’un système en choisissant adéquatement les polynômes R, S, et T, qui doivent répondre à l’équation suivante : R(z−1)⋅Y(z)=S(z−1)⋅U(z)+T(z−1)⋅V(z)R(z^{-1}) \cdot Y(z) = S(z^{-1}) \cdot U(z) + T(z^{-1}) \cdot V(z)R(z−1)⋅Y(z)=S(z−1)⋅U(z)+T(z−1)⋅V(z) Où :
- R(z−1)R(z^{-1})R(z−1) est le polynôme associé au régulateur,
- S(z−1)S(z^{-1})S(z−1) est celui associé au correcteur,
- T(z−1)T(z^{-1})T(z−1) est celui lié à la commande.
L’objectif est de déterminer ces trois polynômes de manière à assurer que la sortie Y(z)Y(z)Y(z) suive une consigne donnée tout en minimisant l’impact des perturbations V(z)V(z)V(z) sur le système.
B. La détermination des polynômes R, S et T
Les polynômes R, S et T sont choisis de manière à satisfaire à des critères de stabilité et de performance, notamment le rejet des perturbations, la minimisation de l’erreur de suivi et l’atteinte d’une réponse dynamique rapide.
III. Comparaison avec d’autres méthodes de régulation
A. Commande PID vs RST
La commande PID est sans doute la méthode de régulation la plus couramment utilisée en automatisation. Elle se base sur trois termes : proportionnel, intégral et dérivé, pour ajuster la sortie d’un système. Cependant, bien que simple à mettre en œuvre, la commande PID peut montrer ses limites face à des systèmes complexes ou soumis à de fortes perturbations. La commande RST, quant à elle, offre une flexibilité supérieure en permettant de modéliser le comportement du système via des polynômes et de le réguler de manière plus précise.
B. Avantages de la commande RST
- Flexibilité : Les polynômes R, S et T offrent une plus grande latitude de réglage que les paramètres PID, permettant d’adapter plus finement la réponse du système.
- Robustesse : La commande RST est particulièrement efficace pour les systèmes qui subissent des perturbations fréquentes ou importantes.
- Adaptabilité : Elle permet de modéliser des systèmes à comportement complexe et de proposer des solutions de régulation adaptées.
IV. Applications pratiques de la commande RST
A. Utilisation dans l’industrie
Dans l’industrie, la commande RST est utilisée pour réguler des processus complexes comme le contrôle de la température, de la pression ou de la vitesse de moteurs. Par exemple, dans les systèmes de production d’énergie, il est essentiel de maintenir des niveaux de tension ou de fréquence stables malgré des variations dans la demande ou dans les conditions environnementales. La commande RST permet d’ajuster la réponse du système en temps réel tout en minimisant les pertes d’énergie.
B. Commande RST dans l’aéronautique
Les systèmes de contrôle des avions, notamment les systèmes de vol automatique, sont des exemples typiques de l’application de la commande RST. Ces systèmes doivent répondre rapidement aux changements d’altitude, de vitesse et de direction tout en maintenant la stabilité de l’avion. La commande RST permet de garantir une réponse optimale tout en tenant compte des perturbations atmosphériques.
C. Application dans l’automobile
Les systèmes de contrôle dans les véhicules modernes, tels que les systèmes de freinage antiblocage (ABS) ou le contrôle électronique de la stabilité (ESC), utilisent des techniques de commande avancées comme la RST pour garantir une sécurité et une performance maximales.
V. Conception et mise en œuvre de la commande RST
A. Les étapes de la conception
La conception d’un régulateur RST repose sur plusieurs étapes :
- Modélisation du système : Le système à contrôler est modélisé sous forme d’équations différentielles ou de fonctions de transfert. Cette étape est cruciale pour déterminer les polynômes R, S et T.
- Détermination des spécifications : Les spécifications de régulation, comme le temps de réponse, la stabilité et le rejet des perturbations, sont fixées.
- Calcul des polynômes : Les polynômes R, S et T sont calculés de manière à satisfaire les spécifications.
- Simulation et validation : Une simulation du système avec le régulateur RST est réalisée pour valider les performances du système.
B. Les outils de simulation
Des outils de simulation comme MATLAB/Simulink sont souvent utilisés pour la conception et la validation des régulateurs RST. Ces logiciels permettent de simuler le comportement du système en temps réel et d’ajuster les polynômes en fonction des résultats obtenus.
VI. Les défis et limites de la commande RST
A. Complexité de mise en œuvre
La commande RST, bien que flexible et puissante, peut être plus complexe à mettre en œuvre que d’autres méthodes, notamment en raison de la nécessité de modéliser précisément le système et de calculer les polynômes R, S et T.
B. Sensibilité aux perturbations
Bien que la commande RST soit efficace pour rejeter les perturbations, elle peut être sensible à des changements brusques dans le système. Par exemple, si la dynamique du système change de manière significative, il peut être nécessaire de recalculer les polynômes.
C. Coût de mise en œuvre
La mise en œuvre d’une commande RST peut nécessiter des ressources supplémentaires, notamment pour la modélisation et la validation du système, ce qui peut entraîner des coûts plus élevés par rapport à des solutions plus simples comme la commande PID.
VII. Perspectives d’avenir
A. RST et intelligence artificielle
Avec les avancées en matière d’intelligence artificielle et de machine learning, il est envisageable de voir une intégration de ces technologies dans les systèmes de commande RST. Par exemple, des algorithmes d’apprentissage automatique pourraient être utilisés pour ajuster dynamiquement les polynômes R, S et T en fonction des conditions réelles du système.
B. Commande RST pour les systèmes non linéaires
Une autre direction de recherche concerne l’application de la commande RST à des systèmes non linéaires. Aujourd’hui, la plupart des applications de la commande RST se limitent à des systèmes linéaires ou faiblement non linéaires. Cependant, des progrès récents montrent qu’il est possible d’étendre cette technique à des systèmes plus complexes.
Conclusion
La commande RST est une méthode puissante et flexible pour la régulation des systèmes dynamiques. Elle offre des avantages significatifs par rapport à d’autres techniques de régulation, notamment en termes de robustesse, de précision et d’adaptabilité. Bien que sa mise en œuvre puisse être plus complexe, elle reste une solution idéale pour des systèmes nécessitant un contrôle précis et fiable.